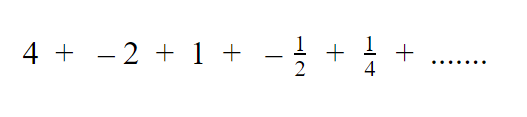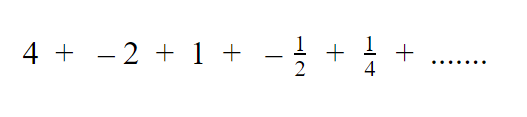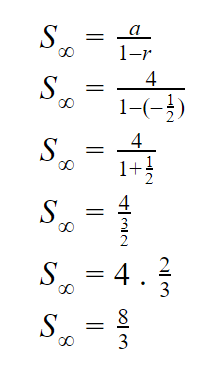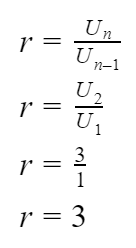E- LKPD Matari Program Linear
Berikut link E- LKPD materi Program Linear yang dapat diakses melalui liveworksheets:
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
Latihan soal deret aritmatika
.png)
LATIHAN SOAL DERET ARITMATIKA
Nama :
Kelas :
Mata Pelajaran : Matematika
Hari, tanggal :
SOAL
1. Seorang petani semangka mengambil buah di sawahnya setiap hari dan selalu mencatat hasil petiknya. Ternyata setelah didata, petani semangka tersebut di hari ke-n memenuhi rumus deret Un=50+25n. Berapa jumlah semangka yang berhasil dipanen ketika mencapai 10 hari pertama?
2. Dalam suatu gedung pertemuan ada 20 baris kursi dengan baris paling depan tersedia 20 kursi. Kemudian setiap baris belakangnya terdapat 3 kursi lebih banyak dari baris di depannya. Maka hitunglah jumlah kursi di baris ke 15!
3. Anita sebagai seorang penjual kain selalu mendapatkan keuntungan dengan jumlah yang sama setiap kenaikan bulan. Apabila di bulan ke-4 Anita mendapatkan keuntungan 30 ribu dan hingga bulan ke-8 memperoleh 172 ribu, maka berapa keuntungannya hingga bulan ke-18?
.png)
.png)
Deret geometri tak hingga divergen dan deret geometri tak hingga konvergen
Deret geometri tak hingga itu dibagi menjadi 2 jenis yaitu deret geometri tak hingga divergen dan deret geometri tak hingga konvergen. Keduanya memiliki perbedaan yang cukup penting. Yuk, kita lihat pengertian dari kedua jenis deret geometri tak hingga tersebut beserta perbedaannya!
Deret Geometri Tak Hingga Divergen
Deret geometri tak hingga divergen adalah suatu deret yang nilai bilangannya semakin membesar dan tidak bisa dihitung jumlahnya. Bisa kita lihat seperti di bawah ini,
1 + 3 + 9 + 27 + 81 + ……………
Kalau ditanya berapa sih, jumlah seluruhnya? Jumlah seluruhnya tidak bisa dihitung karena nilainya semakin besar.
Deret Geometri Tak Hingga Konvergen
Berbeda dengan deret geometri tak hingga divergen, deret geometri tak hingga konvergen merupakan suatu deret di mana nilai bilangannya semakin mengecil dan dapat dihitung jumlahnya. Seperti di bawah ini:
Lalu bagaimana cara menghitung jumlah seluruhnya dari deret geometri tak hingga konvergen?
Rumus Stak hingga pada Deret Geometri Tak Hingga Konvergen
Sebelum masuk ke rumus, ada syarat terlebih dahulu jika kamu bertemu dengan deret geometri tak hingga konvergen, yaitu rasionya harus bernilai antara -1 sampai 1 (-1 > r > 1) dan ini berlaku untuk negatif dan positif. Contohnya seperti deret di atas. Deret di atas rasionya adalah
sehingga bisa dihitung jumlah tak hingganya.Nah, sekarang kita lihat yuk rumus untuk menghitung Stak hingga atau jumlah tak hingganya!
Misalnya kita punya deret geometri tak hingga konvergen:
Lalu, kita coba cari Stak hingga nya, maka:
Jadi, Stakhingga dari deret geometri tak hingga konvergen tersebut adalah
.Itu dia penjelasan tentang deret geometri tak hingga. Bagaimana, teman-teman? Kamu sudah paham, kan? Semoga paham ya, enjoyy..
.png)
Apa sih Deret Geometri itu?
.png)
Setelah mempelajari barisan geometri pada artikel sebelumnya. selanjutnya kita akan mempelajari apa sih Deret Geometri itu? Seperti apa bentuknya dan bagaimana rumusnya? Simak artikel berikut ini, ya!
Nah, kalau barisan geometri dituliskan dalam bentuk penjumlahan, namanya jadi deret geometri.
Deret geometri itu bentuk penjumlahan dari barisan geometri. Penulisannya adalah seperti ini:
1 + 3 + 9 + 27 + …
Kita sudah mengenal pengertian serta contoh dari deret geometri. Sekarang, kita belajar rumus-rumusnya, ya! Pada artikel sebelumnya kita sudah mengetahui rumus rasio dan rumus Un barisan geometri dan deret geometri. Nah, kali ini kita akan bahas rumus Sn. 
Misalnya kita punya barisan geometri:
1, 3, 9, 27, 81, ….
Lalu, kita coba cari Sn nya. Misalnya n yang mau dicari adalah 3, maka:
Jadi, S3 dari barisan geometri tersebut adalah 13.
Oke, itu dia rumus Sn dalam barisan geometri dan deret geometri. See you for the next article....
.png)
Apa sih barisan geometri itu?
.png)
Yuk, kita mempelajari barisan geometri! Seperti apa bentuknya dan bagaimana rumusnya? Simak artikel berikut ini, ya!
Apa sih barisan geometri itu? Apa sih, perbedaannya dengan barisan aritmatika? Oke, supaya kamu nggak bingung, yuk langsung baca penjelasannya di bawah ini!
Barisan geometri adalah pola yang memiliki pengali atau rasio yang tetap untuk setiap 2 suku yang berdekatan. Rasio pada barisan geometri biasa disimbolkan dengan r. Barisan geometri juga biasa disebut sebagai barisan ukur.
Contoh lebih mudahnya begini, misal kamu punya barisan seperti ini:
1, 3, 9, 27, …
Dari barisan tersebut, kita bisa lihat antara suku pertama dengan suku kedua, antara suku kedua dan suku ketiga dan seterusnya selalu punya pengali yang tetap, yaitu 3. Dengan demikian, barisan ini termasuk barisan geometri.
Tadi, kita sudah mengenal pengertian serta contoh dari barisan geometri. Sekarang, kita belajar rumus-rumusnya, ya!
Pada barisan geometri dan deret geometri, terdapat tiga rumus yang harus kamu ketahui, yaitu rumus rasio, dan rumus Un. Kita bahas satu per satu, ya!
Rumus Rasio pada Barisan dan Deret Geometri
Misalnya kita punya barisan geometri:
1, 3, 9, 27, 81, ….
Suku pertama (a) dari barisan geometri tersebut adalah 1. Maka r-nya adalah:
Jadi, rasio dari barisan geometri tersebut adalah 3.
Sekarang kita pelajari rumus suku ke–n (Un), yuk!!
Rumus Un pada Barisan Geometri
Un adalah suku ke-n pada barisan dan deret. Untuk mencari Un pada barisan geometri, kamu bisa menggunakan rumus berikut ini.
Misalnya kita punya barisan geometri:
1, 3, 9, 27, 81, ….
Lalu, kita coba cari Un nya. Misalnya n yang mau dicari adalah 6, maka:
Un = ar^n-1
U6 = ar^5
U6 = 1 . 35
U6 = 1 . 243
U6 = 243
Jadi, U6 dari barisan geometri tersebut adalah 243.
Mudah kan, rumusnya? Syaratnya adalah kamu harus mengetahui berapa nilai a dan r-nya. Dengan begitu, kamu sudah bisa mencari Un dengan mudah.
.png)
Apa sih deret aritmatika itu ?
.png)
Deret aritmatika adalah jumlah n suku pertama (Sn) dari barisan aritmatika. Ciri deret aritmatika adalah suku-suku bilangan yang dijumlahkan memiliki selisih tetap. Contohnya adalah 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + …, dan seterusnya.
.png)
Apa sih barisan aritmatika itu ?
.png)
Barisan aritmatika adalah barisan atau urutan bilangan yang memiliki selisih tetap. Contohnya seperti pada pembukaan artikel ini, yaitu urutan bilangan 1, 3, 5, 7, 9, 11, 13, 15, dan seterusnya. Jika diperhatikan, selisih antarbilangannya selalu tetap, yaitu 2. Selisih pada barisan aritmatika disebut sebagai beda atau dinyatakan secara matematis sebagai b.
websiteku
MathClass (https://mathclass05.blogspot.com/) merupakan blog matematika yang dibuat pada tahun 2024 oleh Erli Puspita Purnama. Blog ini dibuat sebagai bahan ajar yang menarik khusus tentang Matematika.
Dalam blog ini termuat Materi, Modul Ajar, LKPD, dan Video Pembelajaran yang bisa diakses oleh guru dan siswa sebagai contoh bahan ajar. Selain itu, ada juga fitur mengakses latihan soal yang bisa diisi pengunjung untuk berlatih mengerjakan soal-soal Matematika.
Blog MathClass dirancang semenarik mungkin agar pengunjung tertarik untuk selalu mengakses blog ini sebagai website pembelajaran yang mendukung proses pembelajaran. Untuk saat ini, materi dalam blog ini terbatas hanya pada Barisan dan Deret saja, namun kedepannya penulis akan mengusahakan untuk selalu mengupdate materi pada laman blog ini.
Tentang Saya
Halo sobat MathClass... Saya Erli Puspita Purnama, yang saat ini sedang menempuh Pendidikan Profesi Guru (PPG) sebagai wadah melatih profesionalitas guru. Saya lulusan dari S1 Pendidikan Matematika Universitas Bengkulu. Saya lahir di Seluma, 05 Januari 2002. Blog ini saya buat sebagai bahan teman-teman semua untuk belajar materi Barisan dan Deret Fase F SMA/MA. Blog ini dibuat dengan bentuk semenarik mungkin agar pembelajaran bisa diakses dengan menyenangkan.